Магия Геометрии: Исследование Углов с Помощью Формулы Пифагора

В мире геометрии существует множество методов и формул для вычисления углов, но одна из самых универсальных и мощных – это формула Пифагора. Хотя эта формула обычно ассоциируется с прямоугольными треугольниками и длинами их сторон, она также может быть использована для вычисления углов между различными линиями и плоскостями. Давайте глубже погрузимся в эту удивительную тему и узнаем, как формула Пифагора может помочь нам в изучении углов.

Изучение Сущности Формулы Пифагора

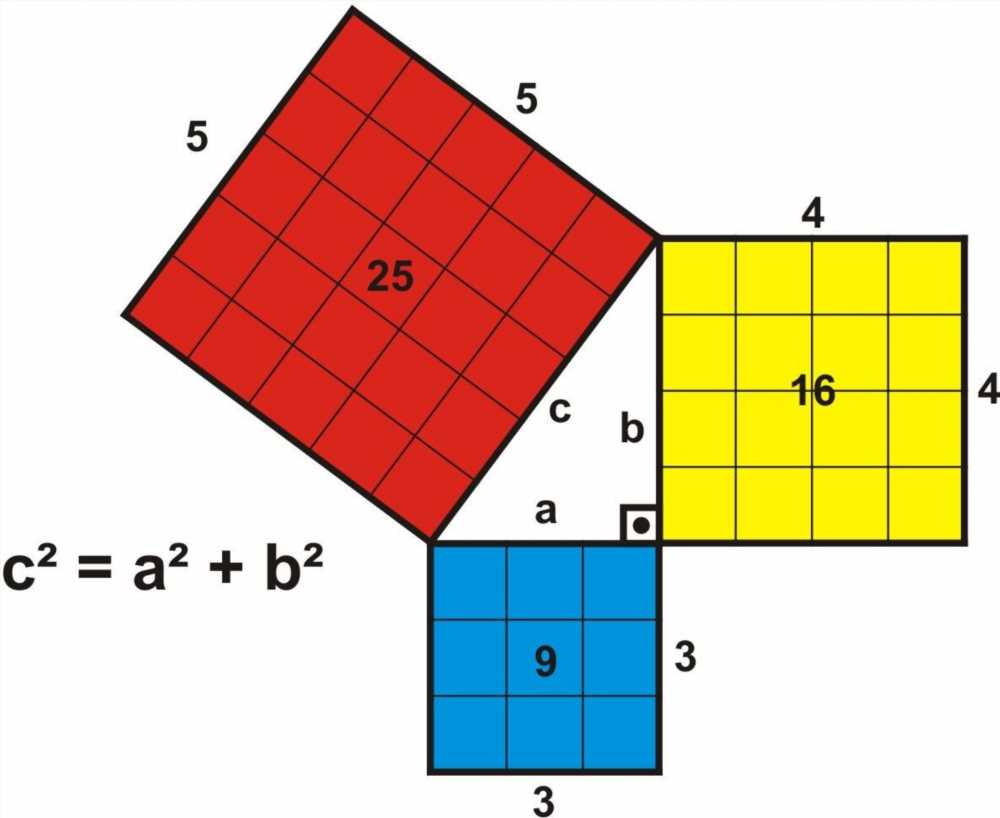
Формула Пифагора, одно из величайших открытий в математике, гласит, что в прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов. Это выражается уравнением:

a^2 + b^2 = c^2

Где a и b - длины катетов, а c - длина гипотенузы. Эта формула может быть использована для нахождения любой из сторон треугольника, если известны две другие, и для проверки того, является ли треугольник прямоугольным.

Применение Формулы Пифагора к Вычислению Углов

Однако, что если нам нужно вычислить угол между двумя линиями или плоскостями? Здесь мы также можем воспользоваться формулой Пифагора, но с некоторыми изменениями.

1. Угол Между Линиями:

Представьте, что у нас есть две пересекающиеся линии, и мы хотим найти угол между ними. Мы можем использовать координаты точек пересечения и длины отрезков, проведенных от точек пересечения до начала координат, чтобы применить формулу Пифагора. Затем мы можем использовать тангенс угла, чтобы найти сам угол.

2. Угол Между Плоскостями:

Аналогично, если нам нужно найти угол между двумя плоскостями, мы можем использовать формулу Пифагора для нахождения расстояния между ними. После этого мы можем применить тригонометрические функции для вычисления самого угла.

Примеры Применения Формулы Пифагора для Вычисления Углов

1. Угол Между Двумя Линиями:

Предположим, у нас есть две линии с координатами и точками пересечения: (1, 2) и (3, 4). Мы можем найти длины отрезков до начала координат: √(1^2 + 2^2) и √(3^2 + 4^2). Затем, применяя формулу Пифагора, мы находим расстояние между этими точками. Далее, используя тангенс, мы можем найти угол между этими линиями.

2. Угол Между Двумя Плоскостями:

Допустим, у нас есть две плоскости с известными координатами и расстоянием между ними. Мы применяем формулу Пифагора для вычисления этого расстояния, а затем используем косинус угла для определения самого угла между плоскостями.

Заключение

Формула Пифагора, хотя и является фундаментальным инструментом в изучении прямоугольных треугольников, также оказывается полезной для вычисления углов между различными линиями и плоскостями. Ее применение не ограничивается только тригонометрией, что делает ее мощным инструментом в геометрических расчетах. Не стесняйтесь использовать эту удивительную формулу в своих математических и геометрических исследованиях!